こんにちは。ブレインズテクノロジーの岩城です。

こちらの記事は、2部構成でお送りしている、Pythonを使用してのARIMAモデルの作成・予測の流れの整理の後半です。

前半の記事では、ARIMAモデルの基礎を簡単におさらいしました。
後半の記事では、Pythonを使って実際にコードを確認しながら、ARIMAモデルを作成し、予測するまでの流れを説明します。

ARIMAモデルの復習が必要な方は、是非こちらの記事も参考にしてください。

PythonでのARIMAモデルを使った時系列データの予測の基礎[前編]

今回も、少し理論の話が出てきます。 理論の部分は前回に引き続き、こちらの教科書を参考にしています。

沖本竜義(2010), "経済・ファイナンスデータの計量時系列分析", 朝倉書店

きちんと理論を整理したい場合は、是非読んでみてください。

記事執筆時の実行環境は下記の通りです。

実行環境

  • MacBook Pro(13-inch, 2017, Four Thunderbolt 3 Ports)
  • プロセッサ: 3.1 GHz Intel Core i5
  • メモリ: 16 GB 2133 MHz LPDDR3
  • OS: macOS High Sierra (10.13.3)
  • Python 3.6.4
  • statsmodels 0.8.0
  • numpy 1.14.0
  • pandas 0.22.0

PythonでのARIMAモデル作成

説明の流れの整理

それでは、早速モデル作成に入っていきましょう。 先に全体の概要を整理しておきます。

  1. 使用するデータについて
  2. データの特徴の確認
  3. 単位根検定の実施
  4. 総当たり法でのモデル候補探索
  5. 良さそうなモデルの確認と評価
  6. 選択したモデルを用いた予測

はじめにどういうモデルになりそうか確認します。その後、いくつかのパラメータを組み合わせた総当たりでのモデル作成を行い、良さそうな候補を選択した上で、結果を確認します。最後に、今回の選択手法でもっとも良いと思われたモデルを使用して、予測を行います。

なお、一連の流れはJupyter notebook上で行いました。

1. 使用するデータについて

今回は元になるデータのモデルが分かっている上で、総当たりの手法で選択される結果について整理してみることにしました。
データはARIMA(0, 1, 1)として設計しています。差分を取る前の、元のデータの導出式は下記の通りとしました。

　　yt=0.1+yt−1+εt−εt−1

この式は変形すると、

　　yt−yt−1=Δyt=0.1+εt−εt−1

となり、1階差分の系列がc=0.1 、 θ1=−1 のMA(1)過程になるようになっています。誤差項はμ=0 、σ2=25(σ=5) の正規分布としました。

また、最後に日付を利用した予測をさせるので、ここでは架空の日付を作成してデータに付与しておきました。

ここまでのコードは下記の通りです。

import numpy as np
import pandas as pd
import statsmodels.api as sm
import matplotlib.pyplot as plt
import datetime
%matplotlib inline

def create_data(data_length, delta=0, ar1 = 1, ma1 = -1, set_std=1, y0 = 0, random_seed=0):
    np.random.seed(random_seed)
    cur_y = y0
    e_m1 = np.random.normal(loc=0, scale=set_std)
    val_list = []

    for i in range(data_length):
        val_list.append(cur_y)
        e_0 = np.random.normal(loc=0, scale=set_std)
        cur_y = delta + ar1 * cur_y + e_0 + ma1 * e_m1
        e_m1 = e_0
        
    return val_list

# 架空の時間データを作成する。与えた年、月、日から1時間ごとの情報を作成する。
def create_dummy_date(start_info, data_num):
    """
    Args:
        start_info: List of integers, [year, month, day]
        data_num: int, number of data.
    Returns:
        List of datetime.
    """
        
    date_list = []
    time_info = datetime.datetime(year=start_info[0], month=start_info[1], day=start_info[2], hour=0)
    for i in range(data_num):
        date_list.append(time_info)
        time_info = time_info + datetime.timedelta(hours=1)
    return date_list

# データの作成
data_num = 2000
delta = 0.1
coef_a = 1
ma1 = -1
set_std = 5
random_seed=0

base_data = create_data(data_num, delta=delta,coef_a=coef_a, ma1=ma1, set_std=set_std,random_seed=random_seed)
linear_data = [i * delta for i in range(data_num)]

index_info = create_dummy_date([2000, 5,1], data_num)

df_all = pd.DataFrame(index=index_info, columns=["raw", "diff1", "linear"])
df_all["raw"] = base_data
df_all["linear"] = linear_data
df_all["diff1"] = df_all.raw - df_all.raw.shift()

fig, ax = plt.subplots( figsize=(6, 4))
df_all.plot(y=["raw", "linear"], ax=ax)

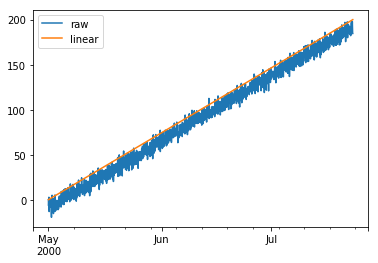
作成したグラフはこちらです。オレンジのラインが比較のための y=0.1t のグラフです。作成したデータはこのグラフに近い位置に存在しています。

f:id:brains_iwaki:20180604175326p:plain

記事の最後で、作成したモデルを用いた予測を行うので、ここでモデル作成用のデータを分けておきます。

df_base = df_all[:1000][["raw", "diff1"]]
raw_data = df_base.raw
diff1_data = df_base.diff1.dropna()

モデル作成用データの先頭3行と末尾3行を確認しましょう。

# データの始めの3行と末尾3行の確認
df_base.head(3).append(df_base.tail(3))
 
 
  raw diff1
2000-05-01 00:00:00 0.000000 NaN
2000-05-01 01:00:00 -6.719476 -6.719476
2000-05-01 02:00:00 -3.726572 2.992904
2000-06-11 13:00:00 91.350700 1.562956
2000-06-11 14:00:00 85.241684 -6.109016
2000-06-11 15:00:00 89.289168 4.047484

このようなデータが、今回のモデル作成の対象になります。

2. データの特徴の確認

次に、作成したデータの時系列的な特徴を確認します。
以下に、元のデータと1階差分をとったデータそれぞれについて、生データ、自己相関関数(ACF)、偏自己相関関数(PCAF) のグラフを示します。

plt.rcParams["font.size"] = 10
fig, ax = plt.subplots(2, 3, figsize=(20, 8))
axes = ax.flatten()
diff_color = "#800000"

axes[0].plot(raw_data)
axes[0].set_title("raw_data")
fig = sm.graphics.tsa.plot_acf(raw_data, lags=40, ax=axes[1])
fig = sm.graphics.tsa.plot_pacf(raw_data, lags=40, ax=axes[2])

axes[3].plot(diff1_data.dropna(), color=diff_color, alpha=1)
axes[3].set_title("diff1")
fig = sm.graphics.tsa.plot_acf(diff1_data, lags=40, ax=axes[4], color=diff_color)
fig = sm.graphics.tsa.plot_pacf(diff1_data, lags=40, ax=axes[5], color=diff_color)
plt.savefig("../output/df_base_info.png", bbox_inches='tight', dpi=120)
 
 

f:id:brains_iwaki:20180604175615p:plain

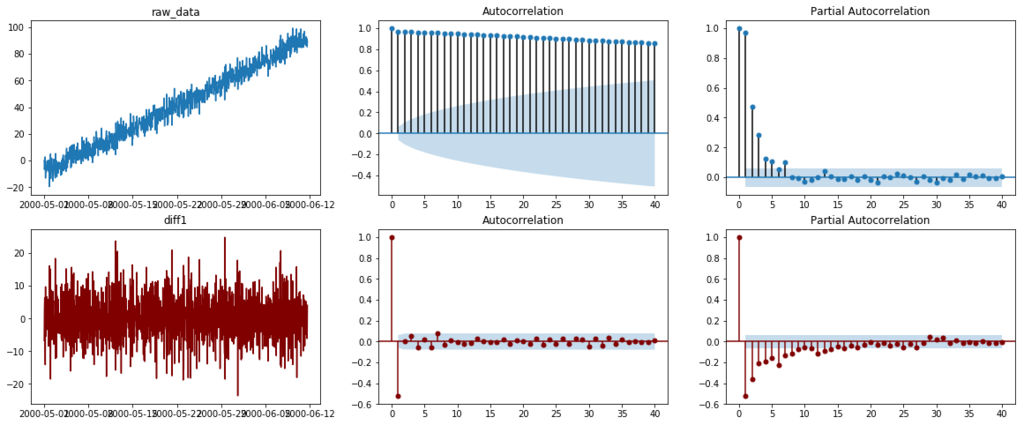
自己相関関数(ACF, Autocorrelation function)と偏自己相関関数(PCAF, Parcial Autocorrelation function)は、任意の時刻のデータyt とそのk個前のデータyt−k の関係性を示す-1 から1の間の値です。

ACFはyk とyt−k との間の線形的な相関の強さを、PCAFはyk とyt−k に対するyt−k 以外の項(yt−k+1 など)の影響を除いた相関の強さを示しています。

細かな説明は参考文献をご参照いただくことにして、グラフから分かることを整理します。
その前に、元データの式と1階差分データの式は下記の通りでした。

　　yt=0.1+yt−1+εt−εt−1
　　yt−yt−1=Δyt=0.1+εt−εt−1

まずは自己相関係数(ACF)の確認をしましょう。

ARのACFの特徴は、一つの項の影響が長期的に減衰しながら残ることです。 例えば、

　yt=ayt−1=a(ayt−2)=a2(ayt−3)=...

のように考えてみると分かりやすいかと思います。このように、ある時刻のデータは、ずっと離れた時刻のデータから表すことができます。

MAのACFの特徴は、MAの次数以降の項が0に近くなることです。これは例えばMA(1)なら、

　　yt=εt−θ1εt−1
　　yt−1=εt−1−θ1εt−2
　　yt−2=εt−2−θ1εt−3

のように式を並べてみると、 yt とyt−2 は直接同じ項を共有していないことが確認できます。このため、直接的な相関関係はない、と考えることができます。
今回は、元データにARの項があり、差分データはMAのみになっているので、ともに期待通りのグラフになっています。

次に、偏自己相関係数(PCAF)です。

AR項の偏自己相関係数は、もともとARの式が次数pの過去の項から構成されていたので、次数pより後ろの項とのPCAFは0になります。 一方で、MA過程は反転可能であればAR(∞)と書き直すことができることもあり、偏自己相関係数も無限に残ることになります。

今回のグラフでは、両方ともMAの項を含んでいることもあり、急激に小さくなるのではなく、減衰していく様子が確認できます。

3. 単位根検定の実施

続いて、単位根検定を行ってみましょう。

その前に、ここで初めて単位根という言葉が出てきたので、まずは定義を確認します。

定義 5.1 (単位根過程)
原系列yt が非定常過程であり，差分系列Δyt=yt−yt−1 が定常過程であるとき，過程は単位根過程(unit root process)といわれる．
(沖本竜義(2010), "経済・ファイナンスデータの計量時系列分析", P. 105, 朝倉書店より引用)

要は、元のデータが非定常過程であり、差分系列が定常過程であるような系列が単位根過程です。今回は1階差分によって定常の式が得られるようにデータを作成したので、検定の結果、単位根過程である可能性を示せることを期待します。

単位根検定を実施する背景には、データが単位根過程であるか、別の過程かによって、作成するモデルの特性や得られる予測が大きく異なってくることがあります。こちらも非常に重要なので、教科書をご参照ください。

単位根検定にもADF検定、PP検定、KPSS検定など、いくつか種類があります。 こちらも詳細は参考文献等をご参照ください。

今回はADF検定を用いることにしました。

ADF検定では、過程が単位根AR(p)であることを帰無仮説とした検定を行います。そのため、棄却されなければ単位根がないとはいえない、という結論になります。なお、単位根検定の際は、仮説のモデルが定数項とトレンドを含むか考慮する必要があります。今回はデータを与えるモデルをこちらで決めていたので、モデル通りの、定数を含む場合での結果を示します。

statsmodelsのadfullerはこちらを参考にしてください。
statsmodels.tsa.stattools.adfuller — statsmodels 0.9.0 documentation

それでは、元データへのADF検定を行いましょう。

# 単位根検定
adf_result = sm.tsa.stattools.adfuller(raw_data)
adf_result

 出力結果は、

    (0.10136608604360935,
     0.9661542394395962,
     18,
     981,
     {'1%': -3.4370334797663844,
      '10%': -2.568341114581742,
      '5%': -2.8644907213150725},
     5938.189071549921)
 
 

となりました。一番初めの値が検定値、2番目がP値です。
期待通り、P値はおよそ0.966で、0.05よりも大きいので、単位根AR(p)過程でないとはいえないという検定結果が確認できました。

4. 総当たり法でのモデル候補探索

今回は総当たり法でモデルの候補を探します。

ちなみに、総当たりを用いずに、データからモデルを考える場合には、先ほどのACF、PCA、単位根検定などを利用して候補を考える方法があります。

その場合は、次数が減衰する位置の確認や検定を組み合わせながら、モデルを考えていきます。
今回の例では1階差分のACFが2次以降で0近くになったので、ARIMA(p,1,1) (p≥1)が候補になりそうですね。

総当たり法では単純に、様々なパラメータでモデルを作成し、AIC等を用いて有力だと思われるモデルを探します。

今回は、p={0, 1, 2}、q={0, 1, 2}, d={0, 1}の各パラメータの組み合わせを試すことにします。

結果の確認のため、作成したモデルのAICを一つのデータフレームに集約させます。
コードは下記の通りです。

# シンプルな総当たり
p_num = 3
d_num = 2
q_num = 3
trial_num = p_num * d_num * q_num
use_columns = ["p", "d", "q", "AIC"]
step_cnt = 0
train_data = raw_data

info_df = pd.DataFrame(index=range(trial_num-2), columns=use_columns)

for p in range(p_num):
    for d in range(d_num):
        for q in range(q_num):
            if p == 0 and q == 0:
                continue
            model = sm.tsa.statespace.SARIMAX(train_data, order=(p, d, q), enforce_invertibility=False, trend='t')
            param_list = [p, d, q]
            for name, val in zip(use_columns[:-1], param_list):
                info_df.iloc[step_cnt][name] = val
            try:
                result = model.fit(disp=False)
                # print(result.aic)
                info_df.iloc[step_cnt]["AIC"] = result.aic
            except:
                pass
            step_cnt += 1
            print("Finish trial No. {}, Param: {}".format(step_cnt, param_list))

AICが低い順番に並べ変えた結果が下記の表です。

 info_df.sort_values(by="AIC")
 
 
  p d q AIC
12 2 0 2 6070.66
3 0 1 2 6085.99
14 2 1 1 6086.7
8 1 1 1 6092.45
5 1 0 1 6126.84
6 1 0 2 6134.79
2 0 1 1 6149.16
11 2 0 1 6218.62
13 2 1 0 6295.7
10 2 0 0 6305.9
4 1 0 0 6423.68
7 1 1 0 6433.19
1 0 0 2 6439.94
0 0 0 1 6511.52
9 1 1 2 NaN
15 2 1 2 NaN

AIC最小のモデルは(2, 0, 2)、2番目が(0, 1, 2)、3番目が(2, 1, 1)、元のモデルのパラメータである(0, 1, 1)は7番目でした。

それではこれらの4つの組み合わせに対して改めてモデルを作成し、結果を確認してみましょう。

5. 良さそうなモデルの確認と評価

先ほどのパラメータを使用したモデルを再作成し、結果を確認します。

良いモデルかどうかは、作成したモデルから出力される結果と実際の値との残差が、平均0、自己相関係数が全て0のホワイトノイズになっているかどうかで判断します。

全ての自己相関係数が0かどうかを判断するには、Ljung-Box検定を使用します。
この検定では、自己相関係数に対してρ1=ρ2=...=ρm=0(1≤m≤k,m は整数) という帰無仮説を立てます。得られたP値から、

  • P値が0.05より小さく、帰無仮説が棄却されれば、kまでの間の少なくとも一つは自己相関係数が0ではない。
  • P値が0.05より大きく、帰無仮説が棄却されなかった場合は、kまでの間の全ての自己相関係数が0ではないとはいえない。

という検定結果を得ることができます。

モデル作成結果の中にもLjung-Box検定の結果は記載されていますが、今回は明示的に検定を行うことにしました。検定の結果を見やすくするために、下記の関数を使用することにします。

# 残差に対するLjung-Box検定
def make_lbtest_df(test_data, lags=10):
    test_result = sm.stats.diagnostic.acorr_ljungbox(test_data, lags=lags)
    lbtest_df = pd.DataFrame({
        "Q": test_result[0],"p-value": test_result[1]})
    lbtest_df = lbtest_df[["Q", "p-value"]]
    return lbtest_df
 
 

(1) (2, 0, 2)でのモデル作成

それでは、まずは総当たりでAIC最小だった(2, 0, 2)のモデルを再度作成し、結果を確認します。

 model202 =  sm.tsa.statespace.SARIMAX(train_data, order=(2, 0, 2), trend='c')
result202 = model202.fit(disp=False)
print(result202.summary())

出力結果は下記のようになりました。

                                Statespace Model Results                           
    ==============================================================================
    Dep. Variable:                    raw   No. Observations:                 1000
    Model:               SARIMAX(2, 0, 2)   Log Likelihood               -3055.083
    Date:                Mon, 04 Jun 2018   AIC                           6122.166
    Time:                        17:07:09   BIC                           6151.612
    Sample:                    05-01-2000   HQIC                          6133.357
                             - 06-11-2000                                         
    Covariance Type:                  opg                                         
    ==============================================================================
                     coef    std err          z      P>|z|      [0.025      0.975]
    ------------------------------------------------------------------------------
    intercept      0.0084      0.042      0.201      0.841      -0.074       0.090
    ar.L1          0.0136      0.017      0.802      0.423      -0.020       0.047
    ar.L2          0.9862      0.017     58.070      0.000       0.953       1.019
    ma.L1          0.1036      0.020      5.301      0.000       0.065       0.142
    ma.L2         -0.8833      0.018    -49.170      0.000      -0.919      -0.848
    sigma2        26.2190      1.187     22.090      0.000      23.893      28.545
    ===================================================================================
    Ljung-Box (Q):                       43.34   Jarque-Bera (JB):                 0.26
    Prob(Q):                              0.33   Prob(JB):                         0.88
    Heteroskedasticity (H):               1.01   Skew:                             0.03
    Prob(H) (two-sided):                  0.90   Kurtosis:                         2.95
    ===================================================================================
    
    Warnings:
    [1] Covariance matrix calculated using the outer product of gradients (complex-step).

  平均値と残差を用いたLjung-Box検定の結果を確認しましょう。

resid202 = result202.resid
print(resid202.mean())
lbtest202 = make_lbtest_df(resid202)
lbtest202.index = range(1, 11)
lbtest202

 

 Mean of residual error is 0.7901548893874051
 
 
  Q p-value
1 5.794679 0.016075
2 6.866166 0.032287
3 7.270120 0.063769
4 13.793465 0.007984
5 14.626877 0.012081
6 16.375478 0.011874
7 20.259926 0.005035
8 20.272314 0.009353
9 20.306049 0.016115
10 20.725448 0.023091

残差の平均は0.8程度でした。また、k=10までのLjung-Box検定結果のP値はいずれも0.05より小さいので、自己相関係数のうち少なくとも一つは0ではないという検定結果となります。

以上の結果から、このモデルは今のところ必ずしも良いモデルとはいえなさそうです。
(p, d, q) = (2, 0, 2)というパラメータの通り、差分を一度も取らないモデルである、ということも関係しているのでしょうか。

(2) (0, 1, 2)でのモデル作成

次は、AICが2番目に小さかった、(p, d, q) = (0, 1, 2)の結果を確認します。

model012 =  sm.tsa.statespace.SARIMAX(train_data, order=(0, 1, 2), trend='c')
result012 = model012.fit(disp=False)
print(result012.summary())

resid012 = result012.resid
print("\nMean of residual error is {}".format(resid012.mean()))
lbtest012 = make_lbtest_df(resid012)
lbtest012.index = range(1, 11)
lbtest012
 
 
SELECT value1, value2 FROM sample_table WHERE hash_key = 1 AND range_key >= 2
    /Users/brainsiwaki/.pyenv/versions/anaconda3-5.1.0/lib/python3.6/site-packages/statsmodels/base/model.py:496: ConvergenceWarning: Maximum Likelihood optimization failed to converge. Check mle_retvals
      "Check mle_retvals", ConvergenceWarning)


                               Statespace Model Results                           
    ==============================================================================
    Dep. Variable:                    raw   No. Observations:                 1000
    Model:               SARIMAX(0, 1, 2)   Log Likelihood               -3015.781
    Date:                Mon, 04 Jun 2018   AIC                           6039.561
    Time:                        18:10:22   BIC                           6059.192
    Sample:                    05-01-2000   HQIC                          6047.022
                             - 06-11-2000                                         
    Covariance Type:                  opg                                         
    ==============================================================================
                     coef    std err          z      P>|z|      [0.025      0.975]
    ------------------------------------------------------------------------------
    intercept      0.0996      0.002     64.571      0.000       0.097       0.103
    ma.L1         -0.9864      0.031    -31.372      0.000      -1.048      -0.925
    ma.L2         -0.0052      0.032     -0.162      0.871      -0.068       0.057
    sigma2        24.3259      1.105     22.019      0.000      22.161      26.491
    ===================================================================================
    Ljung-Box (Q):                       34.17   Jarque-Bera (JB):                 0.22
    Prob(Q):                              0.73   Prob(JB):                         0.90
    Heteroskedasticity (H):               0.98   Skew:                             0.03
    Prob(H) (two-sided):                  0.86   Kurtosis:                         2.96
    ===================================================================================
    
    Warnings:
    [1] Covariance matrix calculated using the outer product of gradients (complex-step).
    
    Mean of residual error is -0.08916347484994207

 

  Q p-value
1 1.313842 0.251700
2 1.396998 0.497331
3 2.765295 0.429245
4 4.687174 0.320927
5 4.750206 0.447120
6 4.932049 0.552557
7 13.140888 0.068749
8 13.630489 0.091920
9 14.180136 0.116060
10 14.187540 0.164608

残差の平均はおよそ-0.09、Ljung-Box検定ではいずれもP値が0.05よりも大きく、帰無仮説は棄却されていません。そのため、残差の自己相関係数がいずれも0ではないとはいえない、という検定結果になります。

モデルとしては悪くなさそうですが、モデル作成時にConvergenceWarningが発生しています。mle_retvalsを確認するようにメッセージが出ているので確認しておきます。

 print(result012.mle_retvals)

 出力結果はこちらです。

 {'fopt': 3.0157805026031124, 'gopt': array([-0.14644907, -0.0001639 , -0.00720694, -0.00082886]), 'fcalls': 355, 'warnflag': 1, 'converged': False}

最後の'converged'がFalseになっています。最尤推定の最適化の際に収束性しないような問題がありそうです。

(3) (2, 1, 1)でのモデル作成

次は、AICが3番目に小さかった、(p, d, q) = (2, 1, 1)の結果を確認します。

 model211 =  sm.tsa.statespace.SARIMAX(train_data, order=(2, 1, 1), trend='c')
result211 = model211.fit(disp=False)
print(result211.summary())

resid211 = result211.resid
print("\nMean of residual error is {}".format(resid211.mean()))
lbtest211 = make_lbtest_df(resid211)
lbtest211.index = range(1, 11)
lbtest211

 

                                Statespace Model Results                           
    ==============================================================================
    Dep. Variable:                    raw   No. Observations:                 1000
    Model:               SARIMAX(2, 1, 1)   Log Likelihood               -3015.019
    Date:                Mon, 04 Jun 2018   AIC                           6040.039
    Time:                        18:09:27   BIC                           6064.577
    Sample:                    05-01-2000   HQIC                          6049.365
                             - 06-11-2000                                         
    Covariance Type:                  opg                                         
    ==============================================================================
                     coef    std err          z      P>|z|      [0.025      0.975]
    ------------------------------------------------------------------------------
    intercept      0.1022      0.005     20.028      0.000       0.092       0.112
    ar.L1         -0.0315      0.032     -0.977      0.329      -0.095       0.032
    ar.L2          0.0089      0.033      0.270      0.787      -0.056       0.074
    ma.L1         -0.9917      0.006   -163.987      0.000      -1.004      -0.980
    sigma2        24.3877      1.111     21.959      0.000      22.211      26.564
    ===================================================================================
    Ljung-Box (Q):                       33.84   Jarque-Bera (JB):                 0.26
    Prob(Q):                              0.74   Prob(JB):                         0.88
    Heteroskedasticity (H):               0.98   Skew:                             0.03
    Prob(H) (two-sided):                  0.85   Kurtosis:                         2.95
    ===================================================================================
    
    Warnings:
    [1] Covariance matrix calculated using the outer product of gradients (complex-step).
    
    Mean of residual error is -0.12554654527010825
 
 
  Q p-value
1 0.000015 0.996934
2 0.000184 0.999908
3 1.281983 0.733416
4 3.151668 0.532772
5 3.285055 0.656130
6 3.398996 0.757356
7 11.631083 0.113362
8 12.315876 0.137657
9 12.860859 0.169004
10 12.871481 0.230946

平均はおよそ-0.12、Ljung-Box検定ではいずれもP値が0.05よりも大きく、帰無仮説は棄却されていません。そのため、自己相関係数がいずれも0ではないとはいえない、という検定結果になります。

このモデルは、それほど悪くはなさそうです。

(4) (0, 1, 1)でのモデル作成

最後に、元データを作成するのに使用した、(p, d, q) = (0, 1, 1)でのモデル作成を行います。

 model011 =  sm.tsa.statespace.SARIMAX(train_data, order=(0, 1, 1), trend='c')
result011 = model011.fit(disp=False)
print(result011.summary())

resid011 = result011.resid
print("\nMean of residual error is {}".format(resid011.mean()))
lbtest011 = make_lbtest_df(resid011)
lbtest011.index = range(1, 11)
lbtest011

 

                                Statespace Model Results                           
    ==============================================================================
    Dep. Variable:                    raw   No. Observations:                 1000
    Model:               SARIMAX(0, 1, 1)   Log Likelihood               -3015.563
    Date:                Mon, 04 Jun 2018   AIC                           6037.126
    Time:                        18:09:38   BIC                           6051.850
    Sample:                    05-01-2000   HQIC                          6042.722
                             - 06-11-2000                                         
    Covariance Type:                  opg                                         
    ==============================================================================
                     coef    std err          z      P>|z|      [0.025      0.975]
    ------------------------------------------------------------------------------
    intercept      0.1000      0.002     66.342      0.000       0.097       0.103
    ma.L1         -0.9923      0.006   -169.478      0.000      -1.004      -0.981
    sigma2        24.4122      1.107     22.045      0.000      22.242      26.583
    ===================================================================================
    Ljung-Box (Q):                       34.11   Jarque-Bera (JB):                 0.21
    Prob(Q):                              0.73   Prob(JB):                         0.90
    Heteroskedasticity (H):               0.98   Skew:                             0.03
    Prob(H) (two-sided):                  0.84   Kurtosis:                         2.96
    ===================================================================================
    
    Warnings:
    [1] Covariance matrix calculated using the outer product of gradients (complex-step).
    Mean of residual error is -0.12792704758113668
 
 
  Q p-value
1 0.950670 0.329549
2 1.037009 0.595410
3 2.404111 0.492870
4 4.300639 0.366845
5 4.366195 0.497983
6 4.532642 0.604989
7 12.781170 0.077623
8 13.305484 0.101762
9 13.867792 0.127106
10 13.874346 0.178801

こちらも平均はおよそ-0.12、Ljung-Box検定でのP値はいずれも0.05より大きく、帰無仮説は棄却されません。よってこのモデルの残差はホワイトノイズに近く、ある程度良いモデルであることが期待できます。

以上、4つのパラメータでモデルの作成と評価を行いました。

最初に試したモデルのように、AICが最小の場合でも、必ずしも理想的なモデルになるとは限らないことも確認できました。また、パラメータによっては収束性に問題が発生する場合があることも確認できました。

6. 選択したモデルを用いた予測

最後に、statsmodelsを使用した場合の予測を行ます。 モデルのパラメータには、総当たり法で3番目にAICが低く、モデル確認の結果も悪くなかった(p, d, q) = (2, 1, 1)を使用します。

statsmodelsのpredictionのうち、in-sample、つまりデータがある部分の予測には、one-step-predictionとdynamic predictionの2種類の方法があります。

one-step-predictionでは、すでにデータがある期間に対しては、データの予測に必要な過去のデータとしては実際のデータを使用します。一方、dynamic predictionでは、モデルによって作成されたデータを利用して次のデータを予測します。

詳しくは下記のドキュメントやチュートリアル等をご参照ください。

それでは、グラフを確認してみましょう。

 pred_start = '2000-06-01'
pred_end = '2000-06-20'
focus_start = '2000-06-01'
dynamic_start = '2000-06-05'
focus_end = pred_end
focus_time = [pred_start, focus_end]

# one-step-ahead forecast
predict211 = result211.get_prediction(start=pred_start, end=pred_end)
predict211_ci = predict211.conf_int()
predict211_mean = predict211.predicted_mean

# dynamic prediction
predict211_dy = result211.get_prediction(start=pred_start, end=pred_end, dynamic=dynamic_start)
predict211_dy_ci = predict211_dy.conf_int()
predict211_dy_mean = predict211_dy.predicted_mean


fig, ax = plt.subplots(figsize=(12, 6))

df_base.raw.plot(color='black', ax=ax)
df_all.iloc[1001:].raw.plot(color='b', ax=ax, alpha=0.5, style="--")

# one-step-ahead forecast
predict211_mean.plot( color='r',ax=ax, label='One-step-ahead forecast')
ax.fill_between(predict211_ci.index,  predict211_ci.iloc[:, 0], predict211_ci.iloc[:, 1], alpha=0.1)

# dynamic prediction
predict211_dy_mean.plot( color='g',ax=ax, label='dynamic forecast')
ax.fill_between(predict211_dy_ci.index,  predict211_dy_ci.iloc[:, 0], predict211_dy_ci.iloc[:, 1], alpha=0.1)

ax.set_xlim(focus_time)
ax.set_ylim([50, 150])
 
 

f:id:brains_iwaki:20180604175648p:plain

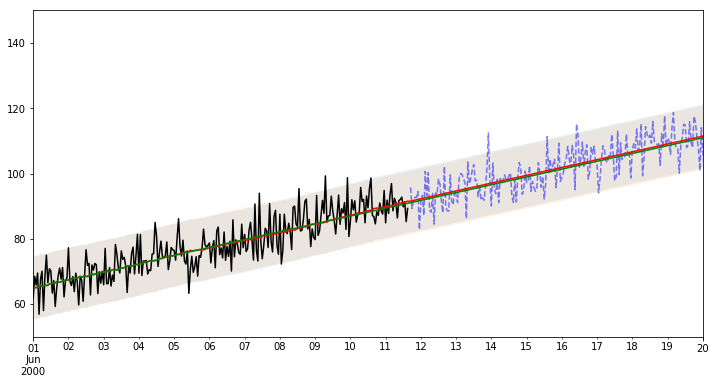
黒の実線が、今回モデル作成に使用したデータを示し、青の破線がはじめに分けておいた、モデル作成に使用していないデータを示します。

予測は赤の実線でone-step predictionの平均値、緑の実線でdynamic predictionの平均値を示し、
95%信頼区間をそれぞれ薄い赤、薄い緑で示しました。今回はこの 2種類の信頼区間がほとんど重なっています。

一部信頼区間から外れていることを含め、この予想結果をどう評価するかは、状況によりけりといったところでしょうか。

まとめ

Pythonのstatsmodelsを用いてのモデル作りから予測までの一通りの流れを行いました。

今回は単純なデータを対象にしましたが、扱った範囲だけでも、次数を試す範囲やモデル選択、モデルの解釈と、検討事項はまだまだ多い印象を受けました。現実のデータでは、季節項やトレンド項、あるいは外的な要因が入ってきたりと、更に難易度が上がっていきそうです。

目的との兼ね合いも考慮しながら、取り入れていけるかどうか検討していきたいと思います。

 

参考文献および参考ウェブサイト